こんにちは!ちいさな桜です。
突然ですが、みなさんは楕円を編むとき、半円部分に何目編み入れるべきなのか、悩んだことはありませんか?
わたしは、楕円の編み地が平らに落ち着きやすい目数は何目なのか、ずっと気になっていたので、今回は「楕円の半円部分のベストな目数」について、考察してみようと思います。
動画でご覧になりたい方はこちら↓


本記事の内容は、完全に自己流のものです。あくまで考察の範囲内で、明確な答えを出すものではないので、その点ご了承ください。
また、本記事は過去記事をもとにしている部分があるため、事前に「円編みの法則」と「楕円の法則」をご覧いただくことを強くおすすめします。
それでは、円編みと楕円、それぞれのベストな目数について、詳しく見ていきましょう。
ベストな目数の定義と結論
本記事では「ベストな目数」の定義を、以下のように定めました。
- 編み地が平らに落ち着くこと
- 編み入れた中心に穴があかないこと
この定義に基づくと、ベストな目数は以下の通りです。
| 円編み(1周) | 楕円(半円部分) | |
| 細編み | 6~8目 | 3~4目 |
| 中長編み | 9~14目 | 5~6目 |
| 長編み | 16~19目 | 6~7目 |
この結論にいたった経緯を、ここから順に説明していきます。
本から読み取れたこと
考察を始めるにあたり、まずは多くの編み物本で使われている目数を調べました。
調査対象は以下の条件で絞り込んでいます。
- 完成形が平らな作品であること
- 初心者向けの本に掲載されていること
上記の絞り込みは、丸みが出る可能性のある作品(バッグ底など)や、複雑な模様編み、レース糸の作品などを除くためのものです。
結果をまとめると、以下の表のようになりました。
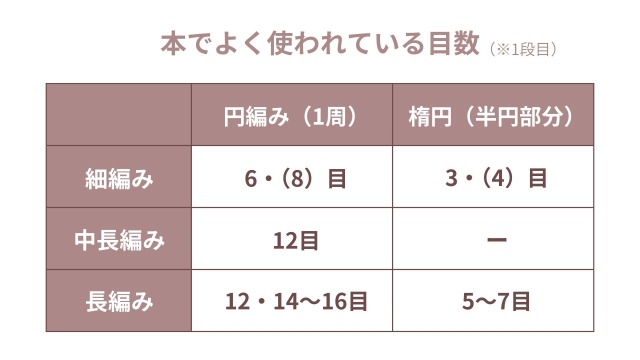
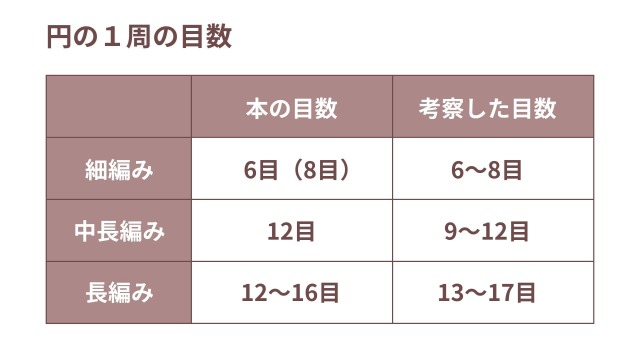
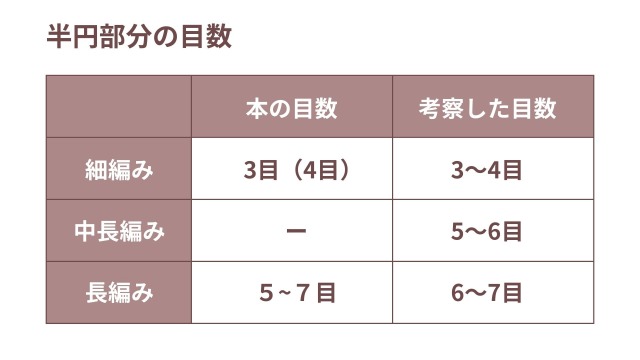
☆本でよく使われている目数(※1段目)
| 円の1周の目数 | 楕円の半円の目数 | |
| 細編み | 6(8) | 3(4) |
| 中長編み | 12 | ー |
| 長編み | 12・14~16 | 5~7 |
※円は1周分、楕円は片方の半円分の目数を表しています。
※細編みの()内の数字は、使用が少ない数字です。
※長編みの円は、13目を除く12~16目です。
※中長編みの楕円はデータが少ないため保留。
この調査結果は、あくまでわたしが調べられた範囲での話ですが、この結果をもとに、以下の4つのことを読み取ることができました。

1.円周の目数は計算できる

編み目には、上図のようにそれぞれ「基準となる高さ」があります。
「円周の目数は計算できる」というのは、この高さを「直径」として考えると、円周の公式(直径×3.14)で必要な目数を計算できるのではないか、という考え方です。

例えば、細編みの高さは鎖編み1目分なので、直径は2目。
2×3.14=6.28目となり、本の一般的な6目とほぼ一致します。
中長編みの高さは鎖編み2目分なので、直径は4目。
4×3.14=12.56目となり、本で一般的な12目と近い値です。

この結果から「編み目の高さと公式で円周は求められる」と考えました。
2.目数は模様編みに左右される
2つ目の推測は「計算で出た小数点以下の数値をどう扱うかは、模様編みへの汎用性が関係しているのではないか」というものです。

例えば、細編みは計算上6.28目ですが、これを切り捨てて6目とするか、切り上げて7目とするかは判断の分かれるところだと思います。
個人的には、7目スタートの方が編み地が落ち着きやすいと感じますが、 本では6目が主流です。
これは、6が2や3で割り切れる汎用性の高い数字であるのに対し、7は素数のため模様編みに対応しにくいことが理由と考えられます。
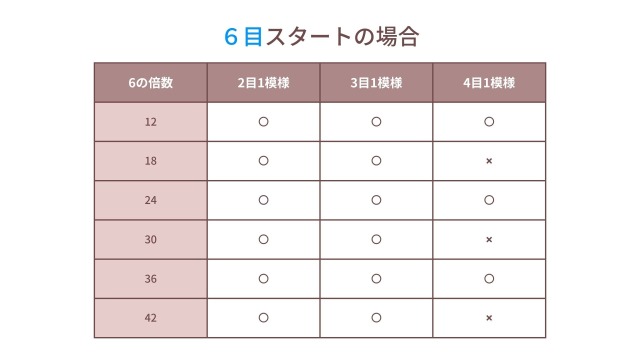
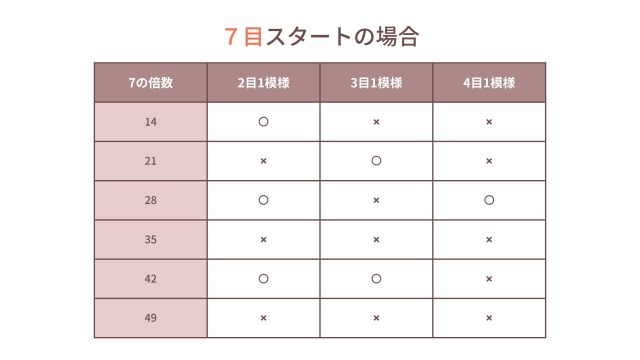
これは中長編みや長編みでも同様です。
12目スタートが多く使われる理由も、13目が「素数」で汎用性が低いため、12目が優先されているのではないでしょうか。
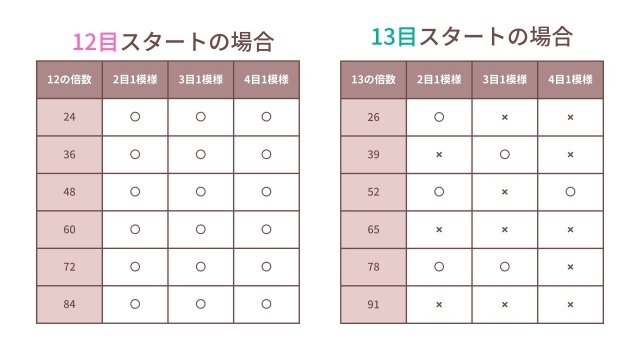
このことから「模様編みに対応しやすい汎用性の高い数字が優先される」と考えました。
3.長編みの円は目数を減らした方が無難
ここまで、計算した円周にほぼ一致していた本の目数ですが、長編みでは計算から外れます。
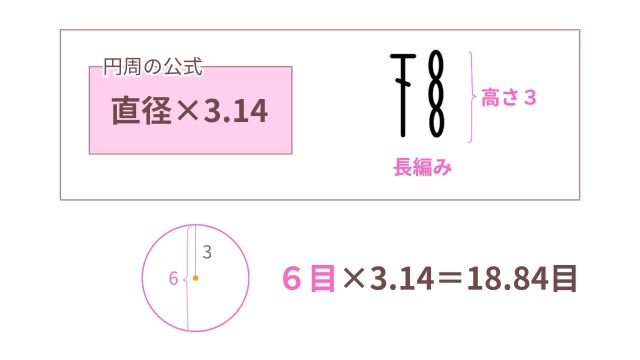
鎖3目分を基準とすると18.84目になりますが、本では計算より少ない12〜16目が一般的です。

この理由は、長編みの編み地の伸縮性にあるのではないかと考えました。多くの本で「長編みは細編みに比べて伸縮性がある」と書かれています。
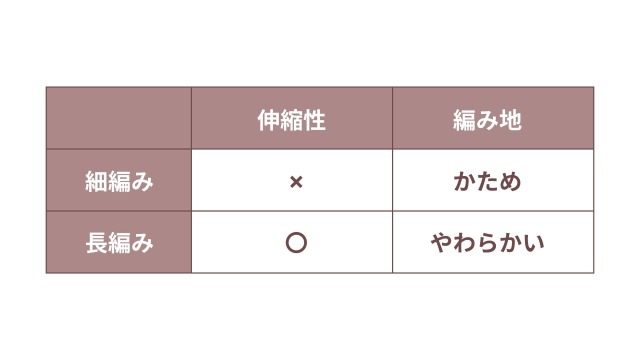
このことから、 長編みは多少目数が少なくても編み地がその差を吸収し、円として成立すると考えられます。
むしろ、中心に穴があくリスクを考えると目数は減らした方が良いと言えるかもしれません。
このことから「長編みの円は目数を減らした方が無難」と考えました。
4.長編みの楕円は円より目数が少なくなる
ここまでの話を、ひとまずあっているものとして、楕円についても考えてみます。
楕円はよく「長方形の両端に半円がくっついている」と表されます。
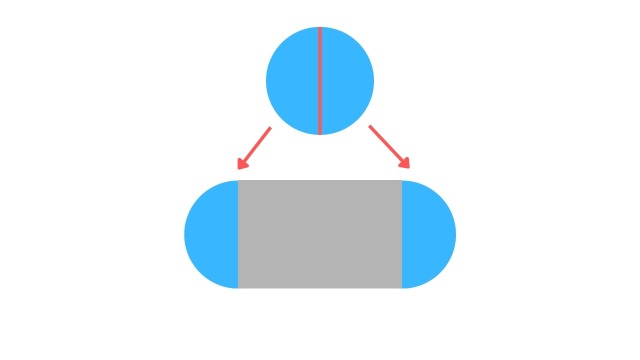
この考えに基づくと、円の目数を半分にすれば、楕円の半円部分に必要な目数になるはずです。
しかし、実際は半分よりもさらに少ない目数になっています。
これには以下2つの仮説が考えられます。
| 中心に穴が空くリスクを避けるため | 編み入れる目数が多すぎると、半円の中心に穴が空きやすくなるため、目数を減らしたのではないか。 |
| 伸縮性による編み地のうねりを抑えるため | 長編みは伸縮性が高く、うねりが出やすいため、計算通りの目数より減らした方が編み地が平らに落ち着くのではないか。 |
この2つが理由で、長編みの楕円は目数が少なくなっているのではないかと考えました。
円を編むときのベストな目数
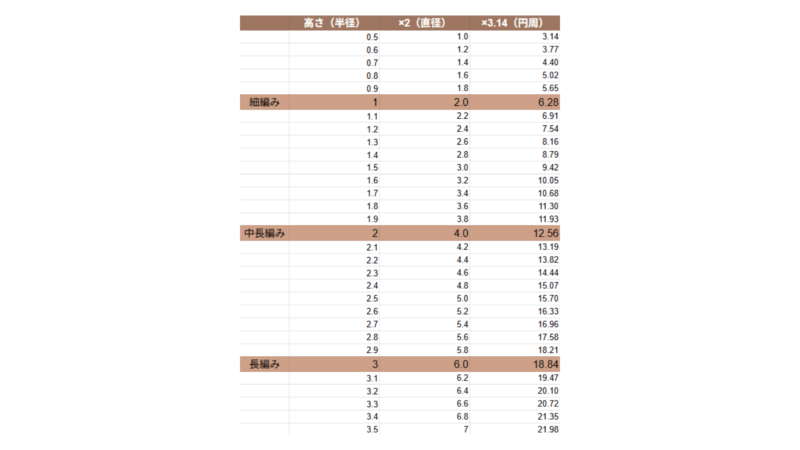

画像は拡大して見てね
ここまでの考察を踏まえ、円を編むときのベストな目数を考えました。
今回は以下のように結論づけています。

- 細編み:6~8目
- 中長編み:9~12目
- 長編み:13~17目
その理由を、細編みから順に、説明していきます。
細編みの円なら6~8目がベスト
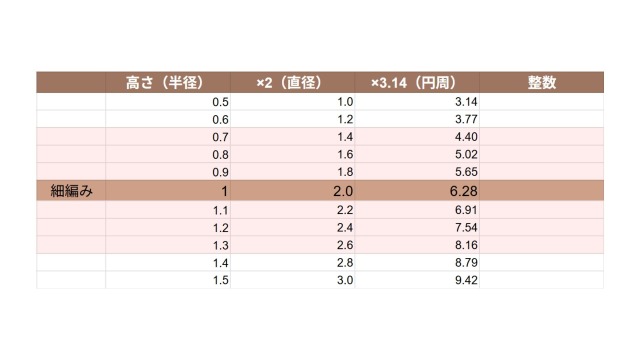

小数点について確認しやすくするため、表を作りました。
細編みの基準の高さが「1」なので、0.9だと足が少し短い細編み、1.1だと少し長めの細編み、ということになります。
細編みの基準の高さ「1」から±0.3の範囲でみてみると、円周は4.4〜8.16目になります。
実際に編むときに小数点はありえないため、これを整数に直すのに四捨五入すると4~8目です。
ただし、四捨五入は範囲に入るか入らないかギリギリのラインにいるような“微妙な数”を範囲に含めてしまう可能性があります。
そのような値はうねりや丸まりが出る可能性が高いと考えられるので、全体的には四捨五入し、下限は切り上げ、上限は切り捨てをして、微妙な数値を含めないよう計算しました。
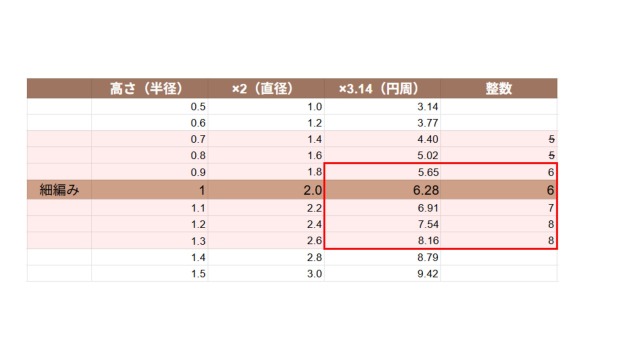

すると、ベストな目数は5~8目となりますが、5目以下は円の形を成さないため省きます。
これにより、範囲が6~8目に狭まったため、今回の考察では、本でよく使われている目数と似た結果になりました。


使い分けとしては、足の長さが短くなりがちなら6目スタート、足が長くなりがちなら8目スタート、模様編みなどを気にしなくて良いなら7目スタートが向いていると言えるかもしれません。
長編みの円なら13~17目がベスト
次は、順番に行くと中長編みですが、先に比較しやすい長編みから考察します。
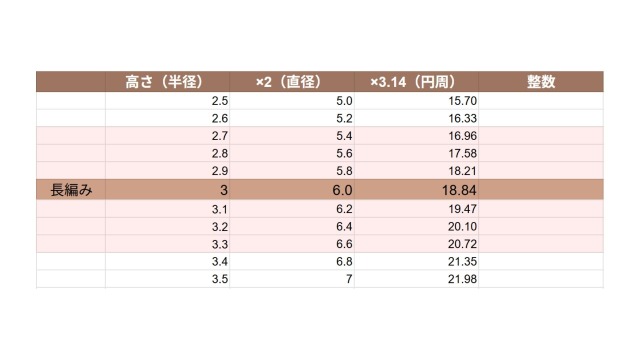

長編みは伸縮性があるため、計算上の値から目数を減らす必要があります。
データをもとに計算したところ、本でよく使われている12~16目は、基準の約60〜90%にあたるとわかりました。
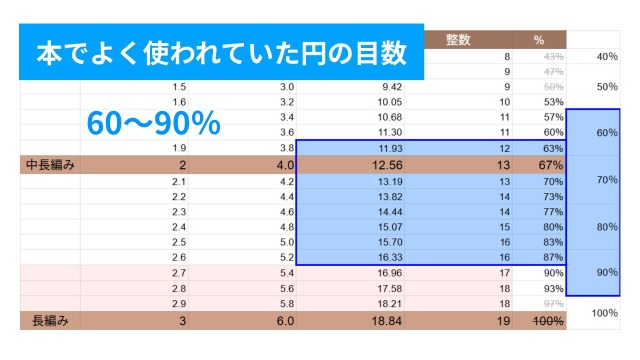

しかし、個人的に60%台は目数を減らしすぎだと感じたため、基準の70〜90%を妥当な範囲と扱いました。
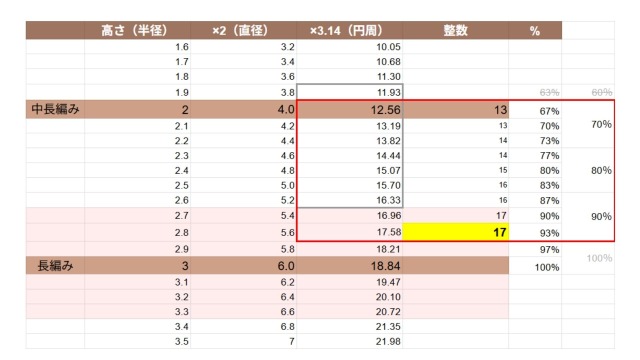

すると12.56〜17.58目が範囲になります。
この範囲を全体的には四捨五入し、下限は切り上げ、上限は切り捨てをして、13〜17目がベストな目数と結論付けました。
中長編みの円なら9~12目がベスト
中長編みは、細編みと長編みの「中間」と考えました。
ここまでの計算では、「細編み:基準どおり」「長編み:基準の70~90%相当」と見当をつけています。
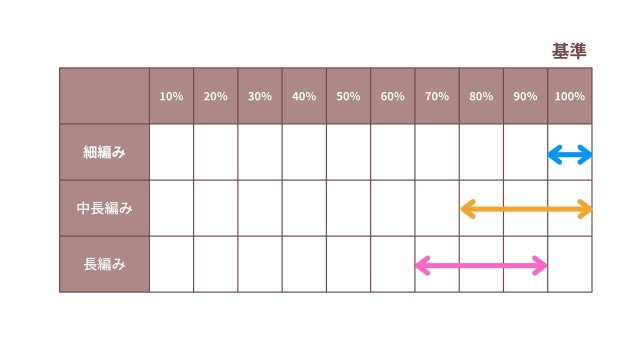

中長編みはその間に位置すると考えると、基準の80~100%相当が妥当なのではないか、と考えました。
表で確認すると、中長編みの基準を100%としたとき、80~100%相当の範囲を求めると、下図のようになります。
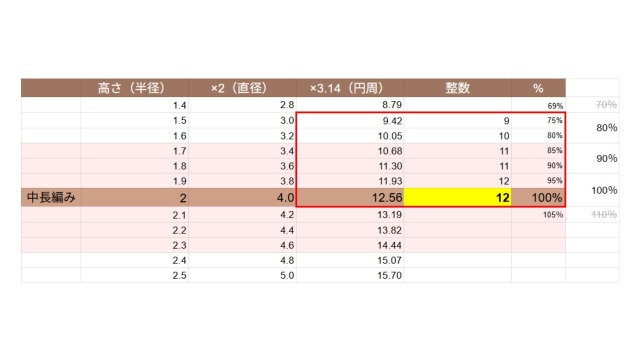

これにより、中長編みの円を編むときのベストな目数は9~12目と、今回は結論づけました。
楕円を編むときのベストな目数
次に、楕円の半円部分のベストな目数を考察します。
冒頭では、楕円の半円部分は以下がベスト、とお伝えしていました。

- 細編み:3~4目
- 中長編み:5~6目
- 長編み:6~7目
理由を、細編みから順に説明していきます。
細編みの楕円なら半円に3~4目がベスト
細編みのベストな目数について、円なら6~8目がベストとしていました。その基になった小数点の範囲は5.65~8.16です。
この5.65~8.16の範囲を2で割ると、2.83~4.08という範囲が求められます。
この範囲の小数点を、基本は四捨五入して、下限は切り上げ、上限は切り捨てすると、3~4目になります。
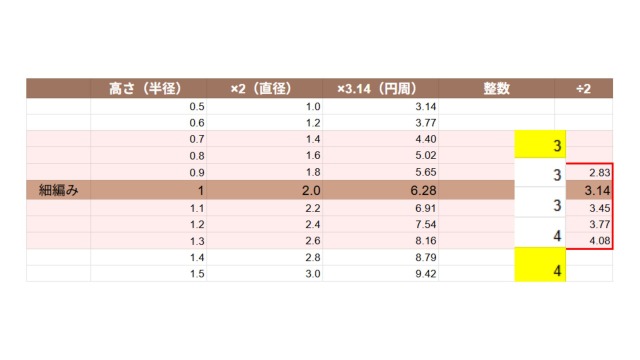

3~4目だと、本の目数とも一致しています。


体感でも妥当と思うので、今回は、細編みの楕円を編むときのベストな目数は3~4目と結論づけます。
長編みの楕円なら半円に6~7目がベスト
次は円と同じく、中長編みより先に長編みについて考察していきます。
長編みの「円」では、ベストな範囲を基準の70~90%相当としていました。
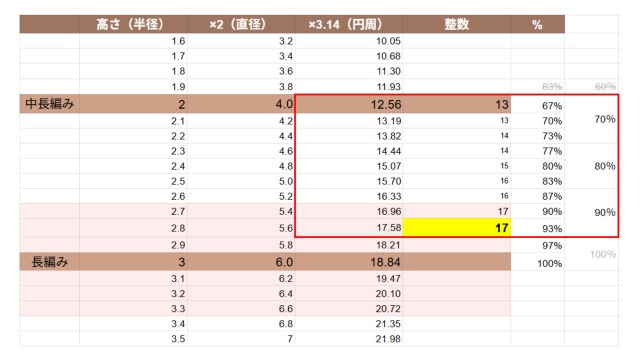

ここからさらに、本から読み取れた「長編みの楕円は円より目数が少なくなる」を加味すると、目数はさらに減るはずなので、10%ほど減らす方向でスライドさせてみます。
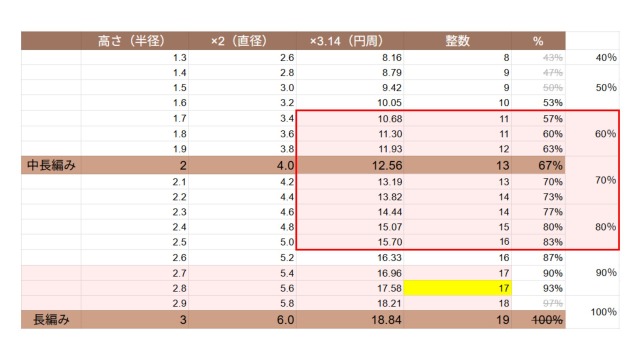

すると、10.68~15.7目が範囲になるため、それぞれ半分にすると5.34~7.85目と求められます。
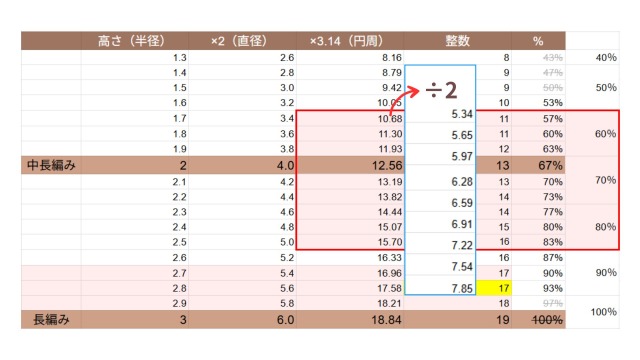

この範囲を、ほかと同じように、基本は四捨五入をして、下限は切り上げ、上限は切り捨てをします。
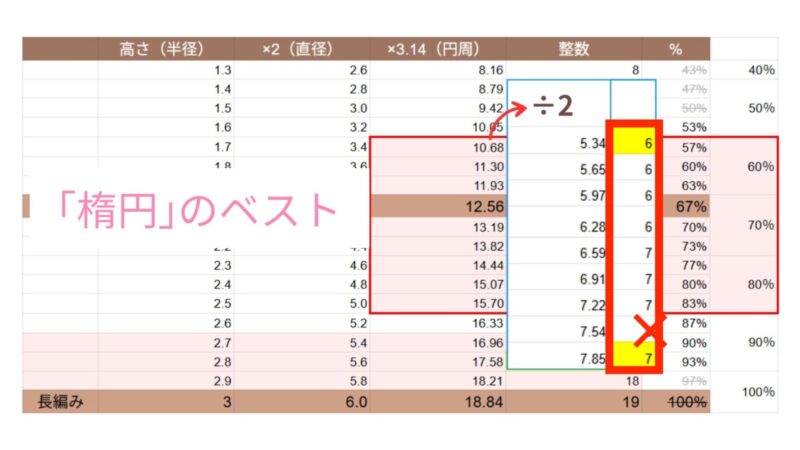
すると、6~7目の範囲の中に8目が登場する、おかしな数字になります。
しかし、そもそも上限と下限を切り捨てや切り上げにしているのは、四捨五入によって「微妙な数字」が範囲に含まれてしまうのを防ぐためでした。
よって今回は、8目を範囲に含めない方向で考え、長編みで楕円を編むとき半円に編み入れるベストな目数は6~7目である、と結論づけました。

中長編みの楕円なら半円に5~6目がベスト
中長編みの楕円は、本でデータが集められなかったため、細編みと長編みの中間として考えます。
まず、ここまでの考察で以下のことがわかっています。
- 細編み:円でも楕円でも基準通り
- 長編み:伸縮性があるため、楕円を編むときは基準の60~80%まで目数を減らす
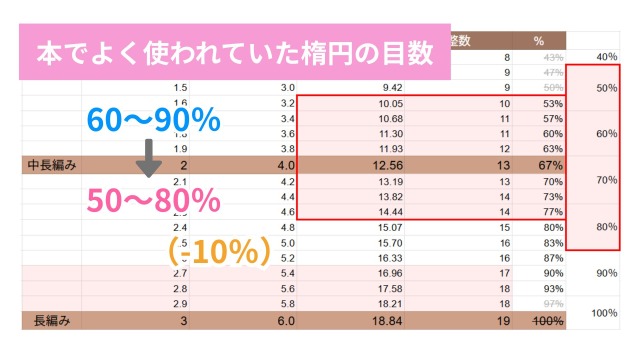
ここで、長編みの60~80%という数値は、本でよく使われている目数の「円から楕円への減り幅」を参考にして割り出した範囲でした。

この減り幅については、長編みの伸縮性や「長編みの楕円は円より目数が少なくなる」という仮説も含めて求めています。
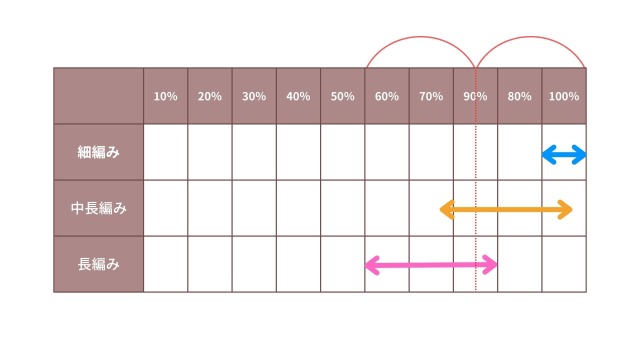
ということは、この長編みの結果については「中長編みよりも目数を減らす要因が多い」といえるため、単純に細編みと長編みの中間になるのではなく「細編み寄り」になることが推測されます。

ここで、参考にした減り幅についてもう一度確認すると、本でよく使われている目数では円より楕円の方がマイナス10%数が減っていました。
“中長編みはそこまで減らさない”とするならば、この差を半分にして「マイナス5%」程度が良いのではないかと考えられます。
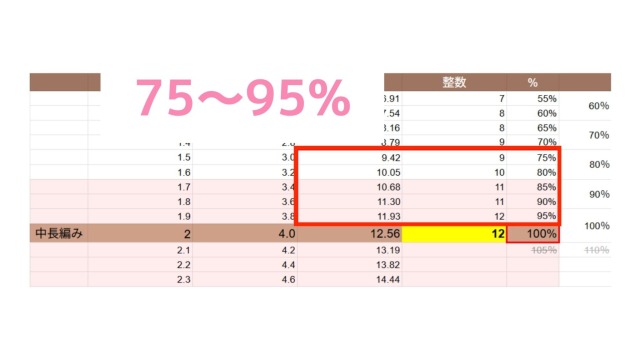

数字でみると、中長編みの基準を100としたとき、ベストな目数は80~100%の範囲としていました。
ここから、-5%になるようにスライドさせると、基準の75~95%相当ということになります。


このときの円周は9.42~11.93目ですので、半円にすると4.71~5.97目となります。
これを、四捨五入と、上限と下限の切り捨て・切り上げをすると、5目、または6目と求められます。
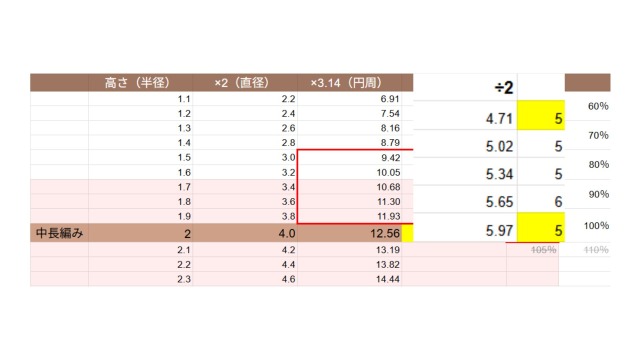

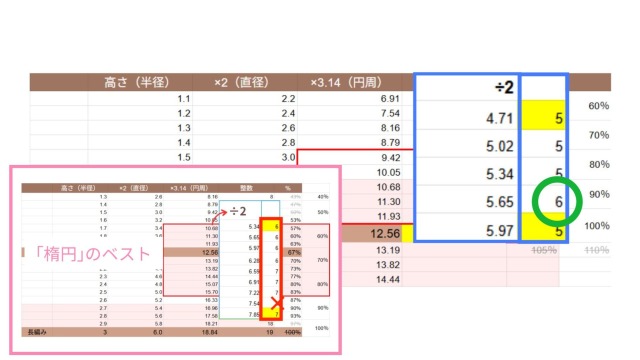
ここで、途中に出てくる上限を越えた目(6目)については、長編みでは範囲に含めていませんでした。
しかし、中長編みの場合、この6目を除外してしまうとベストな目数は5目のみとなってしまい、断定的になってしまいます。
そのため、整合性は取れなくなってしまいますが、ここでは範囲に含めて、中長編みで楕円を編むとき半円部分のベストな目数は5~6目と結論づけたいと思います。

まとめ
今回は楕円の半円部分のベストな目数について考察してみました。
結果はこの通りです。
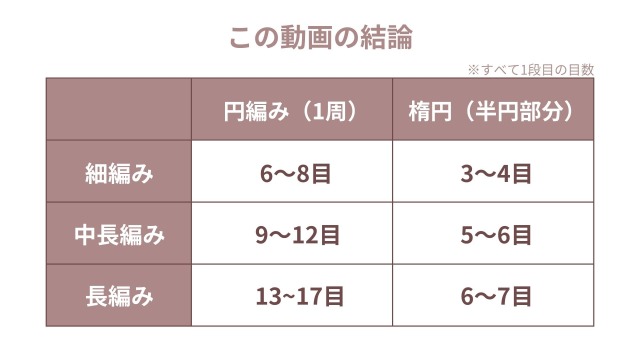

これらの結果は、あくまで個人的な考えにすぎず、正解をお約束するものではありません。
実際は、編むときの手加減や糸の種類によっても、合う目数は変わってきます。
ただ、今回の内容を解説している本を今まで見かけたことがなかったので、同じように悩んでいる方のヒントになれればいいなと思って、この記事を書きました。
あくまで、「私はこう考えたけど、みんなはどう思う?」といった、問いかけや情報共有を目的としています。「これが正解」などとする気は毛頭ありません。
この記事をご覧になって、何か思いついたことなどあれば、ぜひコメントでお聞かせください!
どんなささいなことでも、共有することで、誰かの悩みの解決に繋がる可能性があると思います^^
皆さんの意見をお聞かせいただけるのを、楽しみにお待ちしております☆
最後までお読みいただきありがとうございました。
YouTubeに動画を投稿しています^^
よろしければチャンネル登録よろしくお願いします♪











コメント