こんにちは!ちいさな桜です。
今回は、楕円の編み方シリーズ第一弾として、楕円の法則について、編み図や図形を用いながら考え方を解説します。
動画でご覧になりたい方はこちら↓↓

シリーズは全部で5本あり、第2弾~第4弾が実践編、第5弾は個人的な考察です。
▼第2段
▼第3段
▼第4段
▼第5段
ぜひシリーズ通してご覧いただければ幸いです。
それでは、解説をはじめる前に、2つ補足事項があります。
・補足事項①
今回の内容は、本などには載っていない、完全に「自己流の考え方」です。あくまで、何か参考にできるところがあれば参考にしていただきたいという内容になりますので、その点、ご了承ください。
・補足事項②
この記事では、楕円の基礎は円編みであり、「楕円は円編みの応用」にあたるとしています。先に円編みの動画をご覧いただくことを強くおすすめします。
それでは、楕円の法則について解説していきます。
楕円の法則:7つのポイント
楕円の法則は、以下の順で確認していくと理解しやすいです。

①楕円は長方形の両端に半円がくっついている
②半円の目数の増え方は円編みと同じ
③増し目の位置に決まりはない
④半円の目数は糸や模様に合わせる
⑤楕円の高さは「段数」で調節する
⑥楕円の横幅は「つくり目の数」で調節する
⑦つくり目の数は「横幅-高さ」で決める
こうやって見ると沢山あるように思えますが、このうち①~③が基礎、④以降はオリジナルの楕円を編むときや、アレンジする際に役立つ応用的な内容になります。
まずは①~③をご覧いただき、必要に応じて④以降をご覧いただければと思います。
それでは、順に解説していきます。
①楕円は長方形の両端に半円がくっついている

楕円の構造はいたってシンプルで、長方形の両端に円が半分ずつくっついている、と認識していただければ良いかと思います。
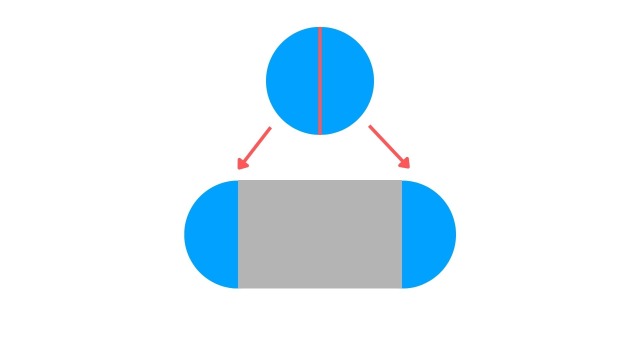
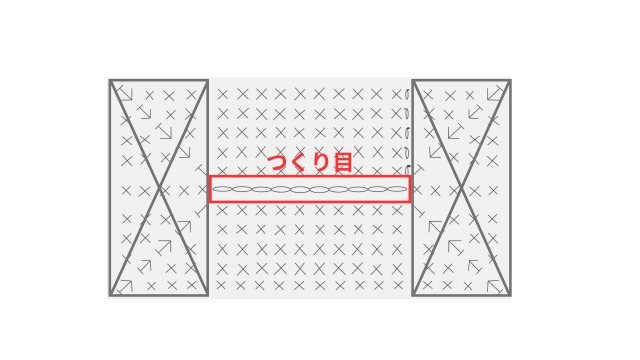
長方形といっても、左辺と右辺は含まずに、つくり目の幅分の長方形にくっつきます。
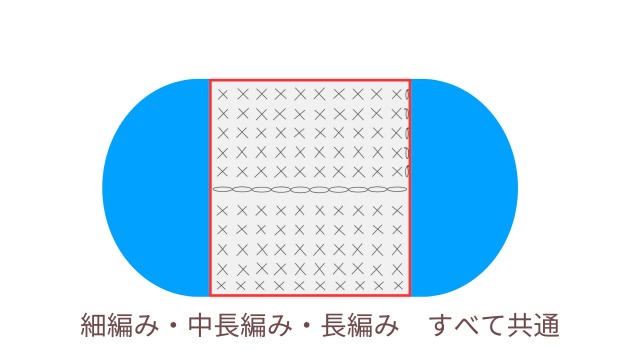
これは、細編み・中長編み・長編みすべての楕円に共通するルールなので、まずはこの点を押さえておいてください。
②半円の目数の増え方は円編みと同じ

次は、両端にくっついた、半円部分の目数がどのように増えていくか解説します。
半円部分の編み方は円編みと同じなので、理解しやすくするために、一度円編みの法則についておさらいしておきたいと思います。
円の法則を解説した記事では、以下のように紹介していました。

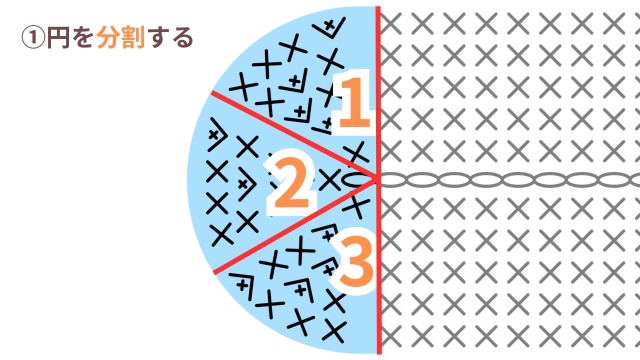
①円を分割する
②各ブロックの法則性は同じ
③必要な目数は段数と等しい
④1周の目数=段×分割数
⑤増し目の位置を分散させる
①円を分割する
「①円を分割する」は、円をスタートの目数で分割して、ブロック単位で考えるということです。
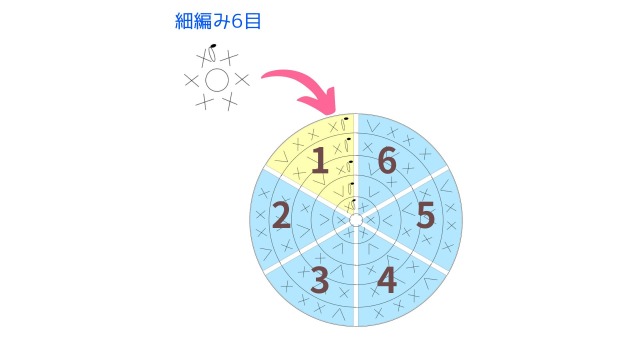
例えば、一般的によく使われる、細編み6目スタートの円なら6分割の円。中長編み12目スタートの円なら12分割の円。長編み16目スタートの円なら16分割の円と考えます。
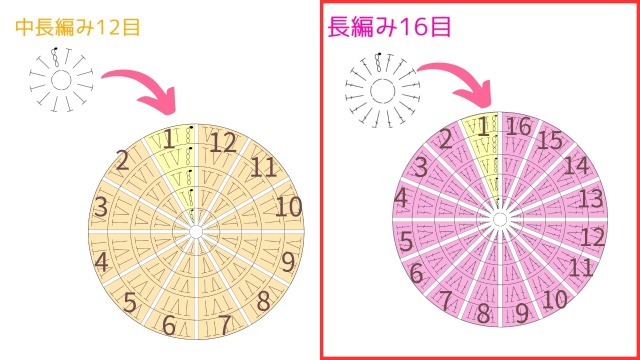
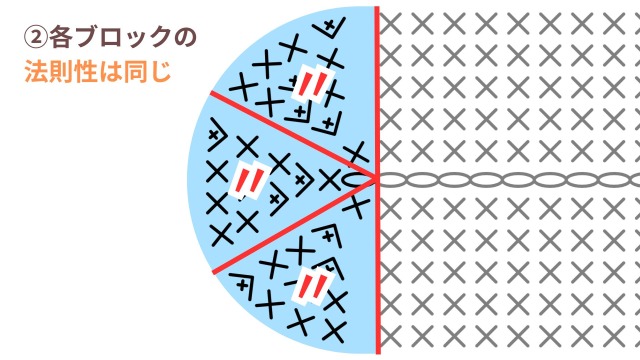
②各ブロックの法則性は同じ
「②各ブロックの法則性は同じ」は、ブロック単位でみれば同じ数ずつ目が増える特徴を指します。
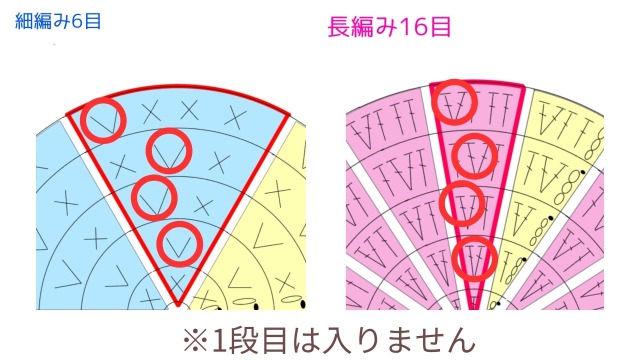
例えば、細編み6目スタートの円を分割してできた1ブロックと、長編み16目スタートの円を分割してできた1ブロックは、以下の画像のように大きさが全然違います。
しかし、ブロック単位でみればどちらも同じ数ずつ目が増えていることがわかります。

これはスタートの目数を変えたり、中長編みで編んだ場合も同様です。
③必要な目数は段数と等しい
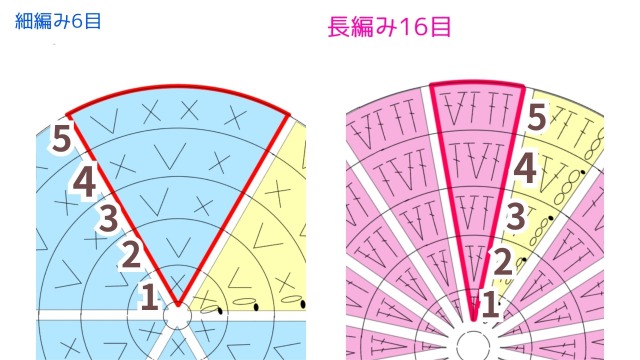
②でどちらも同じ数ずつ目が増えていることがわかりましたが、具体的に、各段何目ずつ編んでいるのかというのが「③必要な目数は段数と等しい」です。
以下の図で見てみると、細編みでも長編みでも、1段目は1目、2段目は2目、3段目は3目入っていることがわかります。
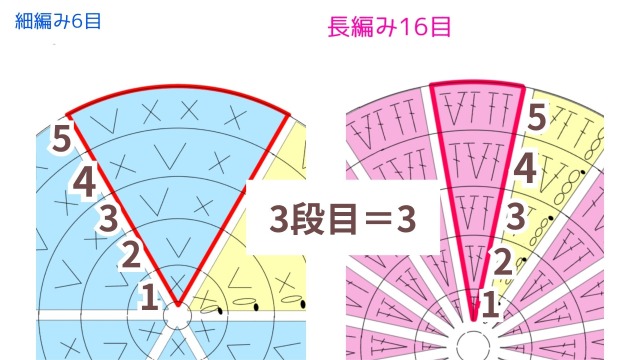

このように、ブロック単位で見ると、編み方に関わらずその段に必要な目数は段数と等しいことがわかります。
編み図ではVのような記号がありますが、これは増し目を意味する記号で、前段の1目に対して2目編み入れることを示しています。
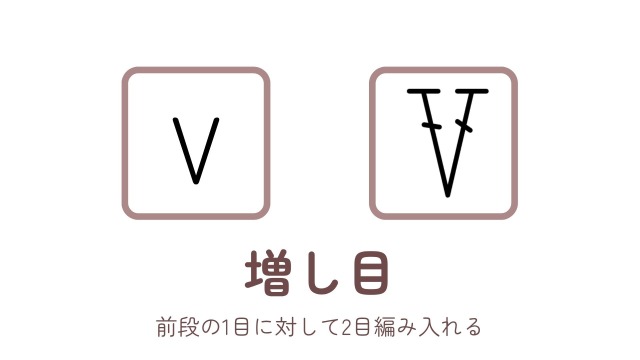

よって、Vの記号1つで2目分になります。
この増し目の記号は、各ブロックで毎段1つずつ入るのが基本です。

例えば3段目だと、1ブロックあたり3目必要なので「1目+増し目」となり、1ブロックあたりの目数は段数と等しく3目になります。
これは以降も共通なので、どのように編んでも「その段で必要な1ブロックあたりの目数は段数と等しい」となります。
④1周の目数=段×分割数
「④1周の目数=段×分割数」は、1周の目数を間違えていないか確かめたいときの計算方法です。
「①円を分割する」と「③必要な目数は段数と等しい」の考え方を組み合わせることで、1周編むのに必要な目数を計算できます。
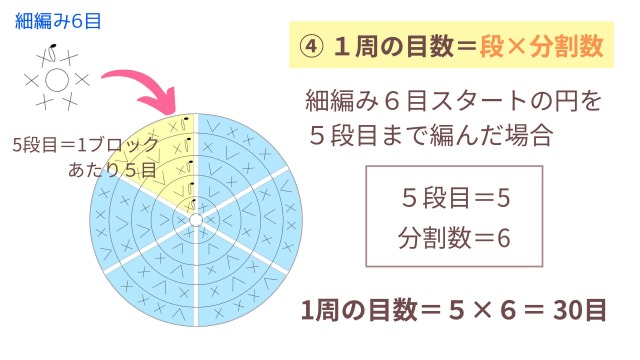

例えば細編み6目スタートの円を5段目まで編んだとして、段は5段目なので「5」、分割数は6目スタートだったので「6」。
「5×6」で、5段目の一周の目数は30目だということが求められます。



次の「⑤増し目の位置を分散させる」については、次の項目で詳しく解説したいので、ここでは説明を割愛します。
楕円に当てはめて確認
ここまでの円編みの法則①~④を、楕円に当てはめて確認しておきましょう。
仮に、以下の図のような楕円があったとして、「①円を分割する」と、半円に3目入っているので分割すると「3ブロック」。

「②各ブロックの法則性は同じ」は、楕円になっても変わりません。

具体的な数では、「③必要な目数は段数と等しい」になるため、ブロック単位でみると1段目=1目、2段目=2目、3段目=3目と、段数と同じ目数が入ります。
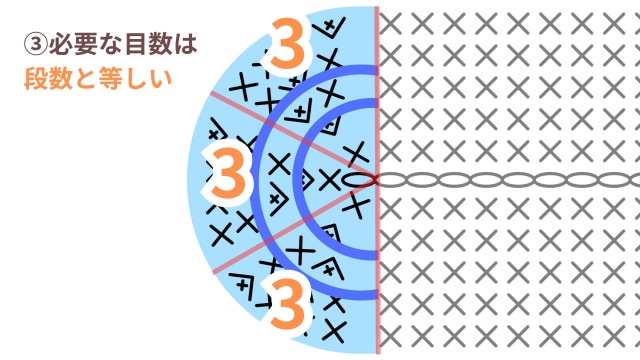

目数を間違えていないか確認するには「④1周の目数=段×分割数」で確認します。
仮に、5段目まで編んだ場合、段は5段目なので「5」、分割数は1段目が3目だったので「3」。
5×3で、5段目の半円部分の目数は、15目で合っていると確認できます。
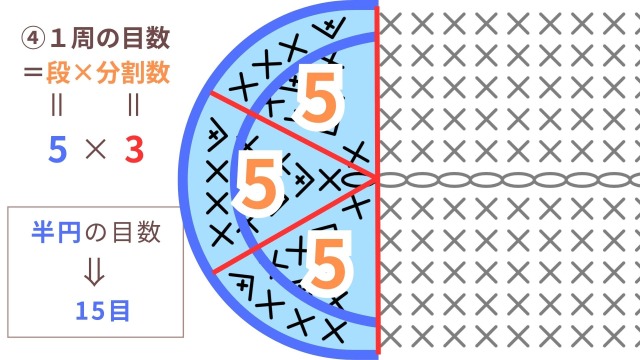

このように、楕円になっても半円部分の目数の増え方は円編みと同じであることがわかります。
ここまでの円の法則についてゆっくり確認しなおしたい方は、以下の元記事をご覧いただければ幸いです。
③増し目の位置に決まりはない


ここからは、前項で割愛した「⑤増し目の位置を分散させる」について触れながら、楕円での増し目の配置について解説します。
まず、円編みでの増し目の位置は「配置は自由だけど、前段と同じ位置にならないようズラす」工夫をするのが一般的です。


これは、増し目には少し盛り上がる特徴があるため、毎段同じ位置で増し目をし続けると角のある円になってしまうためです。


これを避けるには、増し目の位置を分散させればよいため、結果として「前段と増し目が重ならないようズラす」ということになります。
ただ、どれくらいズラすのかは個人の自由なので、デザイナーさんや本によって、色々なバリエーションがあります。
わたしは以下の図のように、偶数段は各ブロックの真ん中、奇数段は各ブロックの左右どちらかの端で編むパターンが多いです。
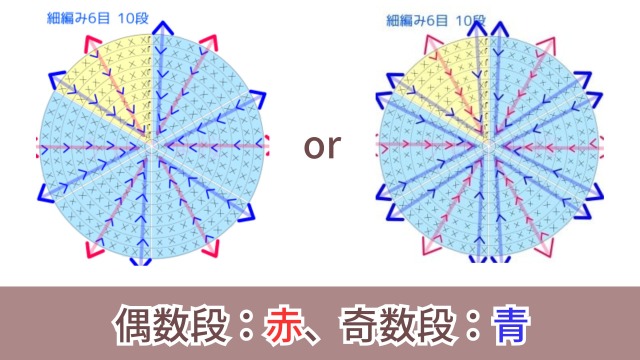




どちらにするかは気分で変えています。
このように、増し目を前段とズラす工夫が「⑤増し目の位置を分散させる」になります。
そして、これは楕円になっても同じです。
円と同じように、前段と重ならないよう増し目の位置をズラせば、キレイな楕円が編めます。
増し目の位置も、自分のやりやすい方法で問題ありません。わたしも、円でも楕円でも同じようなズラし方をしています。
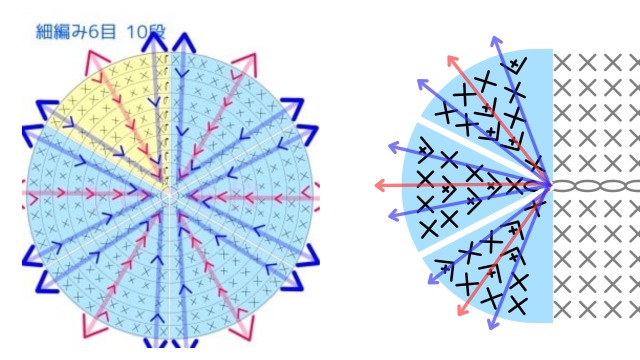

このように、楕円と円はほぼ同じ考え方で編めるといえます。
楕円がわかりにくい理由
ここまで、楕円の考え方は円とほぼ同じだと説明してきました。
しかし、実際は



楕円はよくわからない…
と感じていらっしゃる方も多いように感じます。
ここで、わかりにくくしている原因として、考えられるものは以下2つです。


- 増し目の位置を間違いやすい
- 編み図の規則性がつかみにくい
1つめは、楕円になると半円部分の始まりがわかりにくくなるため、増し目の位置を間違いやすいこと。
2つめは、編み図によっては増し目の位置を大きくズラしていることがあり、規則性がつかみにくい場合があることが考えられます。
1つめに関しては、円編みのリズムのなかに長方形をはさむため、目数を数え間違いやすいのが原因です。これを防ぐ為には、長方形と半円部分の切り替えポイントにマーカーをつけておくと、間違えにくくなります。


この「マーカーをつける」というのは非常に大事で、特に楕円を往復編みするときなどは、最初の目を間違えたために目数が狂うということがよくあります。
往復編みは「(前段で)最後に編んだ目」が「(次の段の)最初の目」になるため、マーカーをつけておくだけで間違いは各段に減らせます。


2つめの「増し目がズレていることにより規則性がつかみにくいこと」。
これは、本来各ブロックに1つずつ配置される増し目が、ブロック内に収まっていない場合を指しています。
以下の画像のように、カーブがきつくなる端に集中して書かれていたり、長方形エリアにも増し目があったりする場合があります。
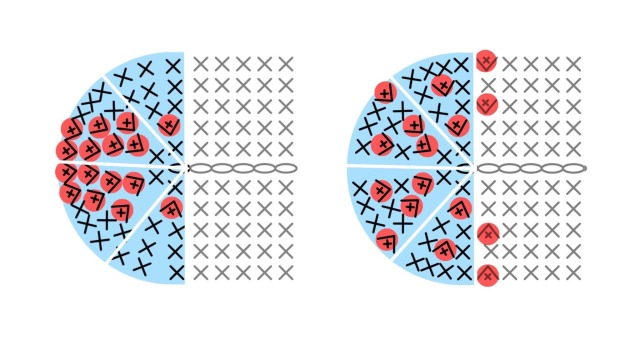

このように、さまざまなバリエーションがあると混乱しやすくなりますが、すべての基本になっているのが「③増し目の位置に決まりはない」ということです。
増し目は絶対にその位置でしないと楕円が成り立たないということはなく、多少ズラしたとしても、カーブを超えるのに必要な目数さえそろっていれば楕円は成り立ちます。
これは先程の、増し目が端に集中しているものや、長方形エリアに編んでいるものも同様です。
どちらも、作家さんが作品の完成度を高めるためにその位置を選んでいるのであって、楕円が成り立つための絶対条件というわけではありません。
部分的にみて目数が計算に合わない場合でも、全体でみれば整合性がとれているということはよくあります。
今まで楕円がよくわからなかったという方は、「必要な目数」と「キレイに編むための工夫」を混ぜて考えてしまっている可能性があります。
「そのエリアに必要な目数がそろっていれば、増し目の位置に決まりはない」ということを意識して、どこかに規則性がないか、色々な角度から編み図を眺めてみると良いかもしれません。
④半円部分の目数は糸や模様に合わせる


ここまでは、半円の各ブロックの内容について解説してきました。
ここからは「そもそも半円に何ブロック配置すべきか」について解説します。



半円部分の1段目は何目編むのが良いかという話です。
この記事はタイトルを「楕円の法則」としているので、絶対に間違いを避ける言い方をするなら「半円に編み入れる目数は糸や模様に合わせる」が正解になるかと思います。
ただ、そうは言っても目安は欲しいので、本でよく使われている目数を、表にまとめてみました。画像(「本の目数」参照)
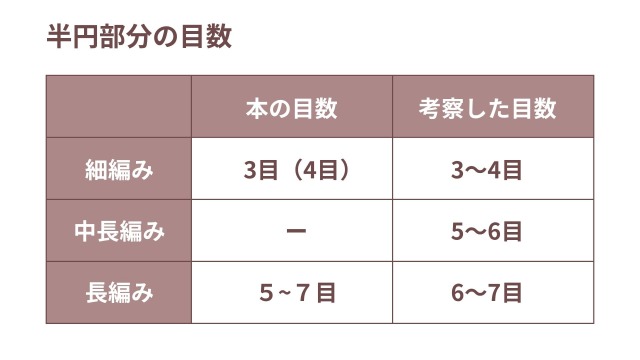

本だと、楕円の半円に編み入れる目数は以下が多い印象でした。
- 細編み:3(or4目)
- 中長編み:(載っている本が少なかったので保留)
- 長編み:5~7目
表の右列の数値は、個人的に考察した半円のベストな目数です。本の目数をもとに、うねりや丸まりを気にせず編める目数について、考察しました。
「本の目数」はあくまで私が調べられた範囲での話です。この数に収まらないケースももちろんありますので、その点ご了承ください。
シリーズ第5段で、この数値を割り出した経緯を紹介しますので、ご興味ある方いらっしゃいましたら、そちらもぜひご覧いただければと思います。
ただ、この記事は「法則」がメインテーマのため、ここでは「半円に編み入れる目数は糸や模様に合わせる」として、終わっておきたいと思います。
⑤楕円の高さは「段数」で調節する


ここからは、楕円の形の変え方を解説します。まずは楕円の「高さ」を変える方法です。
楕円の高さを決める要因は「編んだ段数」のみです。
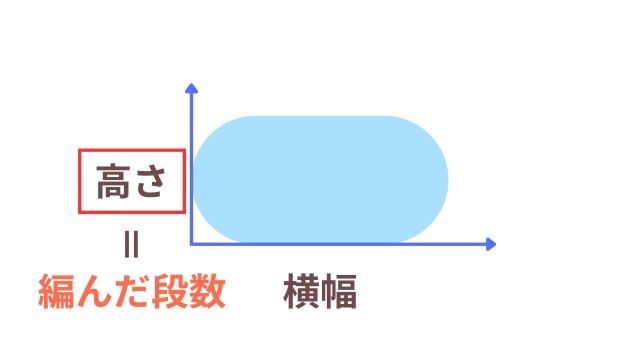

編み図で確認すると、まずつくり目が中心にあり、そこから1段編むと上にも下にも1段ずつ増えます。
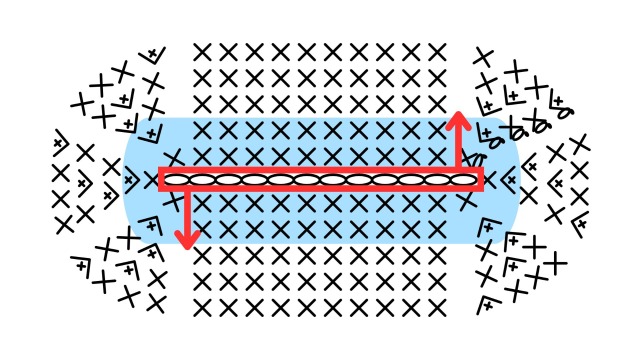

2段目も編むと、上が2段・下も2段となり、合計4段分の高さになります。
このように、楕円の高さは編んだ段数にしか左右されないため、高さを増やしたければ段数を増やせばよいことがわかります。
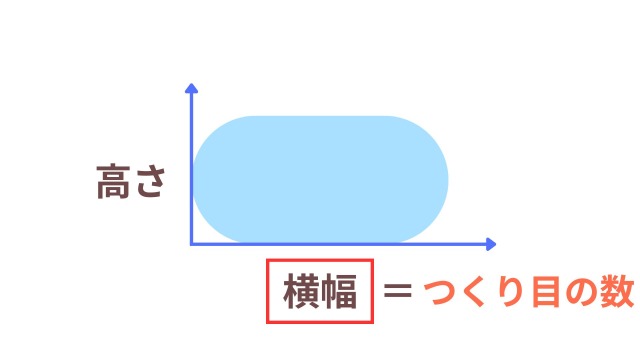
⑥楕円の横幅は「つくり目の数」で調節する


次に、楕円の横幅を変える方法です。楕円の横幅を変えたいときは「つくり目の数」で調節します。

以下の図で確認すると、どちらも細編み5段の楕円ですが、横幅の長さが違いますよね。
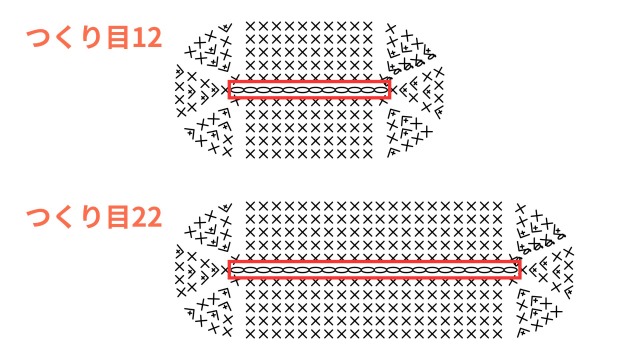

この差を作り出しているのは、最初に編むつくり目の長さです。
上はつくり目が12目、下はつくり目が22目のものです。
このように、楕円の横幅を変えるには、最初のつくり目の長さで調節すればよいことがわかります。
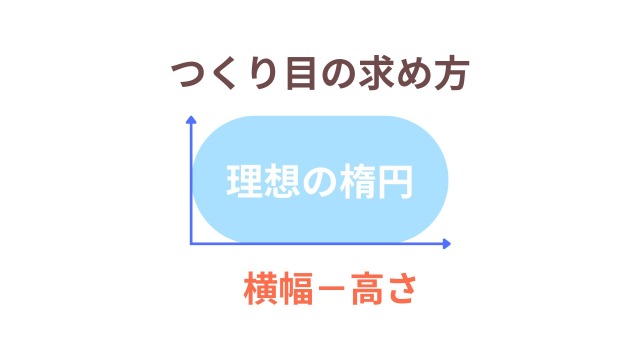
⑦つくり目の数は「横幅-高さ」で決める


⑥の説明で



じゃあつくり目は何目にすればいいの?
と、疑問に思った方もいると思います。
オリジナル作品をつくるとき、つくり目を何目にするかは非常に悩ましいところです。
しかし、考え方はいたってシンプルで、理想の楕円形から「横幅-高さ」をすればつくり目を何目にするかが求められます。

ここまでの説明で、楕円の高さには「編んだ段数しか影響を与えない」という話をしました。
楕円を編むときは、中心からぐるぐると編むため、上に1段増えると自動的に下にも1段増えます。
ここで忘れてはいけないのが、上下だけでなく、自動的に左右にも1段ずつ増えるという点です。
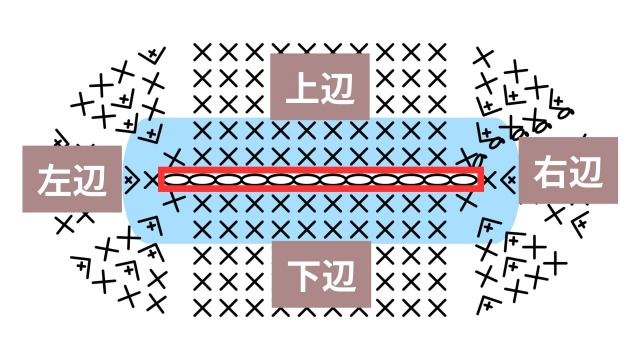

1段編めば、上辺・左辺・下辺・右辺すべてに1段ずつ増えます。



これは段をどれだけ編んでもずっと変わりません。
これを踏まえて、高さ10㎝、横幅30㎝の楕円を編むために必要なつくり目を計算してみましょう。
まず、つくり目の目数が不明でも、つくり目が楕円の中心にくることは決定しています。
すると、実際に編むのは「高さ10㎝」の半分の5㎝分ということが求められます。
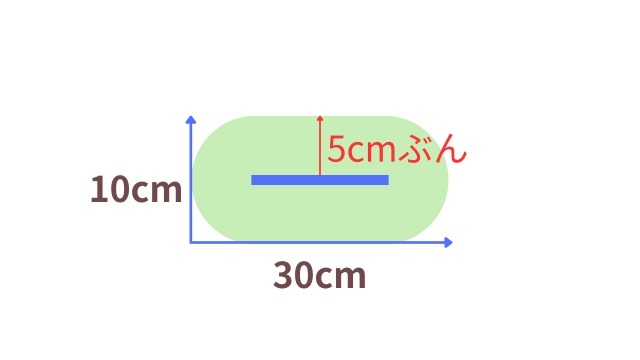

この5㎝の間に何段編むことになるかは、この時点ではまだ分かっていません。
しかし、5㎝ぶん段数を編むことは決定しました。
すると、この時点で、横幅30㎝の左右5㎝ずつも、自動的に埋まることがわかります。
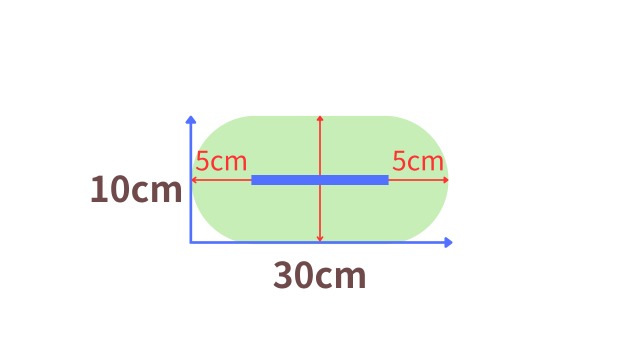




中心からぐるぐる編むから、1段編んだら上下左右すべてに1段増えるよ。
よって、30㎝-左側5㎝-右側5㎝=20㎝ぶんが、空白部分としてあくことになります。
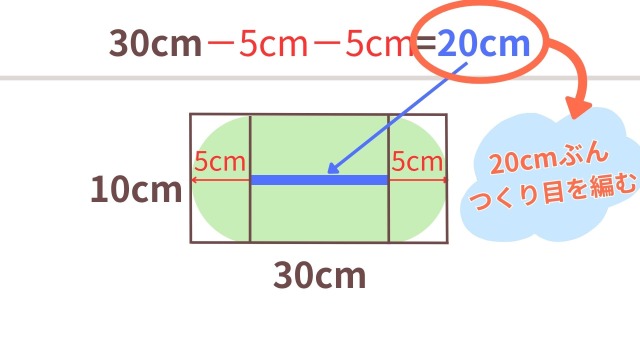

その空白部分をつくり目で埋めてあげれば、この楕円が成立することになります。
空白部分を埋めるために、つくり目が何目必要かは、実際に使用する糸や手加減によって左右されます。
極太糸なら少ない目数で埋まりますし、細いレース糸なら、それなりに鎖を編む必要があります。
この辺りはゲージをとって割り出すのが一番ですが、面倒なら実際に紙に理想の楕円を書いてみて、空白部分にあてながら、随時調節するのがいいのではないかなと思いいます。


今回ご紹介した方法なら、基本的にはどのような糸や編み方でも、つくり目の数を求められます。
ただ、この方法以外にも色々考え方はあると思いますので、あくまで考え方の一例として、お役立ていただければ幸いです。
まとめ


今回は楕円の法則について解説してきました。
楕円は編み方に関わらず、細編み・ 中長編み・長編み、すべて共通した考え方で編めますので、ぜひ難しくとらえず、楽しく編み進めていただければと思います。
楕円解説シリーズ第2弾~第4弾では、それぞれの編み方で、楕円を10段目まで実際に編むところをアップしますので、一緒に編みながら進めたい方は、ぜひそちらもご覧ください。
最後までお読みいただきありがとうございました!
YouTubeにかぎ針編み動画を投稿しています^^
よろしければチャンネル登録よろしくお願いします♪
したらね~♪











コメント